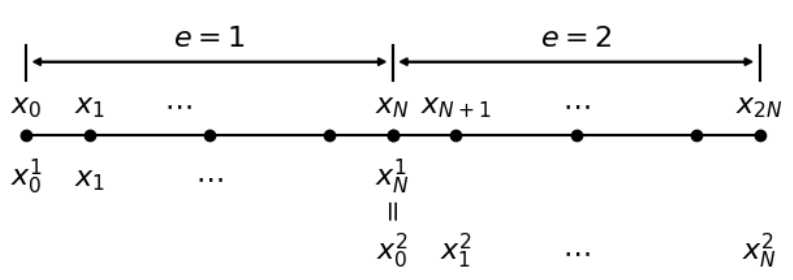In this post, I’d like to talk a bit about how Nek treats the connectivity and therefore periodicity. Despise that we are going into Nek’s structure, the general concept can be applied to other finite elements methods. This is one of the main communication we have in the solver handled by gslib 1 which we will talk about it in the future posts.
1. Formulation
Let’s start with a 1D domain with two elements at polynomial degree $N>0$. The high-order part doesn’t really matter, here we just use that to give each elements $N+1$ points. See the figure below.
The $N$+1 grid points in the left element ($e$=1) are named $x_0^1, x_1^1, \cdots, x_N^1$. As for the right element, we have points $x_0^2, x_1^2, \cdots, x_N^2$. Since two elements are connected, they share a common interface point \(x^1_N = x^2_0\). Therefore, there are only $2N+1$ unique points and we order those unique coordinates with global indices from $x_0$ to $x_{2N}$. On the same coordinates, $x_N = x^1_N = x^2_0$, if there is a continuous function $u(x)$ across the elements we will have $u(x_N) = u(x^1_N) = u(x^2_0)$.
Up to this stage, we have two numbering systems.
| Name | Notations | #Points | #Unique coordinates | |
|---|---|---|---|---|
| Local index (L) | $x_i^e$, $\ \ e=1$ or $2$, $\ \ i=0,1,\cdots,N$ | 2N+2 | 2N+1 | |
| Global index (G) | $x_j$, $\ \ j=0,1,\cdots,2N$ | 2N+1 | 2N+1 |
Based on the collocation points and spatial discretization, one can compute the numerical integration, derivatives or whatever algebraic equations based on the local points within an element. To simplify the problem, let’s say we have discretized linear system for each element.
\begin{align} A^e \underline{u^e} = \underline{f^e}, \ \ e=1, 2 \end{align}
1.1 Numerical Integration Viewpoint
We go back to the weak formulation that seeks the solution $u$ in weak space satisfying the integral norm for arbitrary test function $v$.
\[A[u](v) := \int_\Omega v A(u) = \int_\Omega v f(u) =: F[u](v)\]With two elements $\Omega=\Omega^1\cup\Omega^2$, the integral is simply the sum of each local integrals
\[A[u](v) := \int_{\Omega^1} v A(u) + \int_{\Omega^2} v A(u)\]From the view of the global grid points, the point $x_N$ will naturally have contribution in both integrals in each element.
1.2 Collocation Viewpoint
Two elements will have $2N+2$ equations but the continuity requirement only yields $2N+1$ degree of freedom. Therefore, it’s natural to merge two equation on the common point $x_N$. By adding two equations together, it will achieve the continuity due to the equal contribution form both elements.
1.3 Gather-Scatter Operations
Either way, the combined linear system becomes the following system on global grid.
\[\begin{pmatrix} a^1_{0,0} & a^1_{0,1} & \cdots & a^1_{0,N} & & & & \\ a^1_{1,0} & a^1_{1,1} & \cdots & a^1_{1,N} & & & & \\ \vdots & \vdots & \ddots & \vdots & & & &\\ a^1_{N,0} & a^1_{N,1} & \cdots & a^1_{N,N} + a^2_{0,0} & a^2_{0,1} & \cdots & a^2_{0,N}\\ & & & a^2_{1,0} & a^2_{1,1} & \cdots & a^2_{1,N}\\ &&& \vdots & \vdots & \ddots & \vdots \\ & & & a^2_{N,0} & a^2_{N,1} & \cdots & a^2_{N,N}\\ \end{pmatrix} \begin{pmatrix} u(x_0) \\ u(x_1) \\ \vdots \\ u(x_N) \\ u(x_{N+1}) \\ \vdots \\ u_(x_{2N}) \end{pmatrix} = \begin{pmatrix} f(x_0) \\ f(x_1) \\ \vdots \\ 2f(x_N) \\ f(x_{N+1}) \\ \vdots \\ f_(x_{2N}) \end{pmatrix}\]In practical, such global system should never be constructed. The finite elements arrays are naturally stored in distributed memory for parallel computing so the element-wise data are stored in local arrays.
To transfer between coordinates, we first form the “scatter” operator that copies data from global grid to the corresponding local grid, which can be written in to $Q$ matrix
\[\underline{u}_L = Q \underline{u}_G = \begin{pmatrix} 1 & & \\ & \ddots &\\ && 1 & \\ & & 1 \\ &&& \ddots \\ &&& & 1 \end{pmatrix} \underline{u}_G\]As for the gather operator, it can be treated as the scatter operation from the test function, which is defined as $Q^T$
Solving the global linear system $A_G \underline{u}_G = \underline{f}_G$ is same as solving the local linear system $QQ^T A_L \underline{u}_L = QQ^T\underline{f}_L$ up to the rank = degree of freedom. Despite the values are summed at the interface points, the right-hand-side is also doubled so it still give the same answer after the solve.
One extra detail is, when solving the local system with iterative methods, one has to use either the integral norm or a re-scaled algebraic norm weighted with the inverse of the multiplicity. In other words, the algebraic norm follows the norm in global system.
2. Connectivity
The connectivity is defined as the global index of each points. To construct the $QQ^T$ operator, all it needs is an local array that stores the global index. We assume that both local and global index are continuous and the global one is unique. That is, if it’s 1-base (for MATLAB), the global index starts from $1$ to nUV where nUV is the number of unique points.
1
2
3
4
5
6
7
8
9
10
% Assume both index arrays are continuous
for i=1:length(local_index)
j = global_index(i);
Q(i,j) = Q(i,j) + 1.0;
end
% Or
nV = length(local_index);
nUV = max(global_index);
Q = sparse(local_index,global_index,1.0,nV,nUV);
3. Nek5000’s connectivity
In my opinion, whoever builds the mesh needs to make sure the mesh is water-tight in the sense that there is no leaking holes between elements, or $\Omega = \cup_{e=1}^E \Omega^{(e)}$ where arbitrary two elements has no volume in $d$-th dimension measure $|\Omega^{(i)}\cap\Omega^{(j)}|=0$. This means, one needs to keep track on the connectivity during the meshing. However, meshing is already hard, it will be more flexible if we don’t have to worry about connectivity at each stage. Nek has tools to rebuild the connectivity and user can alter the connectivity in the .usr file as well.
1
2
3
4
5
# Valid Nek5000 inputs
.rea + .map
.re2 + .ma2
.re2 + .co2 + PPLIST+=PARRSB
.re2 + PPLIST+=PARRSB
3.1. .map/.ma2 file and genmap
The genmap is a robust tool that does two things, connectivity and partitioning. We will talk about partitioning in future post.
The algorithm first sorts the coordinates based on their physical coordinates. With an user-provided relative mesh tolerance (default = 0.2), if the distance of two vertices smaller than the criterion, then they share the same node index.
The tol here is an #\epsilon$-ball that can cover the leaking holes in mesh. Therefore, a larger tol is more forgiving to the bad mesh. However, if tol is too large, it can fuse too many points together, which collapses and degenerates the hex elements and causing zero Jacobian value.
The smaller tol can usually get a valid connectivity for high aspect ratio mesh. The “valid” here means runnable in Nek, which doesn’t mean it’s correct. For example, at the limit $tol \to 0$, all elements are treated as isolated subdomains that is not connected to others.
The “isolated” elements is harder to detect but it usually generates an empty boundary condition. The recommendation workflow for genmap is
- Use default tol (0.2) by hitting the return key
- If it fails, tighten the tol
- Repeat 2 until it works, but user must be very careful if tol is, says, less than $10^{-3}$
Keep in mind that, precision matters. If a mesh has high aspect ratio but only stored in ascii .rea format, it might not have enough of precision to use tol-based connectivity tools.
3.2. .con/.co2 file and gencon
The gencon is a subset of genmap that only does the connectivity, so the .co2 file contains only the connectivity. Currently, the .con file is not usable in Nek. We only accept .co2 file.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# symmetric vertex ordering / lexicalgraphical ordering
# in r-s-t coordinates
#
# (vec 15)
# t ^ s (vec 13)
# : .
# : 7 === 8
# : /: /|
# :/ : / |
# 5 === 6 |
# | 3 -|- 4
# | . | /
# |. |/
# 1 === 2 --> r (vec 12)
3.3. n2to3co2 tool
n2to3co2 is a new tool that can extrude a 2D .con/.co2 files to a 3D .co2. It follows the same element ordering in the mesh by n2to3. This tool allow us to generate connectivity for a huge mesh (E = 200M ~ 2Bn) for testing and debugging purpose.
3.4. parCon (shipped in parRSB)
Both genmap and gencon are serial tool. As the problem size gets larger, it can take hours to generate a .co2. Plus, it will need a large RAM server to run it. Personally, if the case is larger than 1M or 10M elements, I’d suggest to use parCon and parRSB.
3.5. setvert and usersetvert
Once the code starts, it reads the global indices of all vertices of the elements and stores it into Nek variable, glo_num. The subroutine setvert in Nek5000 will generate the global indices for each grid points vertex. The indices are numbered in the order of vertices, edges, face, and interior points. At the end of setvert, it calls usersetvert which allows user to modify or overwrite the index. This allows user to do whatever they want to modify the connectivity.
3.6. gs functions
Nek5000 will setup the gather scatter operations based on the connectivity. The $QQ^T$ operations can be done by call dssum(u,lx1,ly1,lz1). Instead of sum, one can also do other reduction operations.
1
2
3
4
dsop(u,'sum',nx,ny,nz)
dsop(u,'mul',nx,ny,nz)
dsop(u,'min',nx,ny,nz)
dsop(u,'max',nx,ny,nz)
One can also look into fgslib_gs_op (gs_op in gslib + prefix for Fortran interface) to see the API in details including data type and many operations.
4. Periodicity
How to do enforce periodicity is one of the most asked questions in Nek5000’s forum.
In the code level, it’s literately zero effort. The periodicity is treated the same as the internal "E " boundary as long as the connectivity is set properly. It’s super easy to achieve (double/triple) periodic, or even complicate topology such as a Möbius strip. Neat!
4.1 genbox and .rea/.re2
The genbox will set the boundary condition "P " in .rea/.re2 and specify the neighbor’s element id and face id into bc(1,f,e,ifield) and bc(2,f,e,ifield). This, however, is a temporary information for the tools like genmap. At runtime, this “face-to-face” connectivity is never used.
One can use this face-to-face connectivity, in my understanding, this is how we deal with the vector-translated periodic, p .
Note: The periodic BC set in the
.boxfile only works when there is a single box. For multi-boxes, one has to fix the periodicity withprenek’s auto-periodic.
4.2 genmap (or gencon)
genmap will read the “face-to-face” connectivity stored in .rea or .re2.
One can directly modified the generated the .co2 file to have desired connectivity.
Note:
genmaprequire 3 layers of elements to identify the periodic with correct orientation. Think about Möbius strip, face-to-face connectivity can still flip the face orientation in 2D.
4.3 usrsetvert
This is called at runtime, which is the last chance to modify the connectivity. In the subroutine usrsetvert (.usr) is called after setup. This allows us get rid of “3 layers of elements” condition. See NekRS example channel
fix_geomwill make sure the grid points sharing the same global vertex are at the same location. However, the points that hasPwill be skipped.